标题：卡尔曼滤波：原理剖析与实时应用探索

引言

卡尔曼滤波器（Kalman Filter）是一种有效的递归滤波器，广泛应用于信号处理、控制系统、机器人技术等领域。它通过最小化估计误差的方差来优化估计值。本文将深入剖析卡尔曼滤波的原理，并探讨其在实时应用中的重要性。

卡尔曼滤波的基本原理

卡尔曼滤波器基于线性系统理论，其核心思想是通过一系列的预测和更新步骤来逐步减小估计误差。以下是卡尔曼滤波的基本原理：

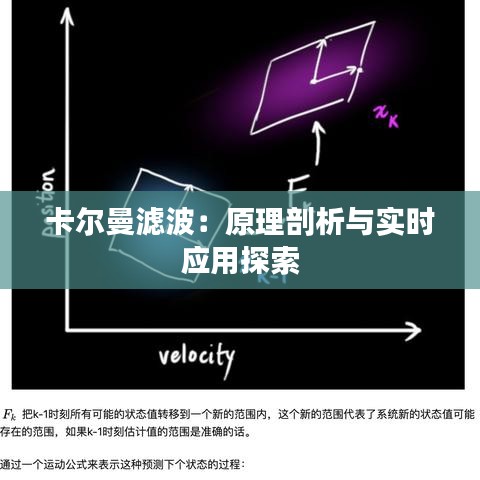
1. 状态空间模型：卡尔曼滤波器将系统状态表示为一个向量，并通过一系列的状态方程来描述状态的变化。状态方程通常包括系统的动态方程和观测方程。

   

2. 预测：在每一时间步，卡尔曼滤波器根据先前的状态估计和系统模型来预测当前的状态。

3. 更新：通过将观测数据与预测状态进行比较，卡尔曼滤波器对预测状态进行修正，以减小估计误差。

4. 协方差矩阵：卡尔曼滤波器使用协方差矩阵来描述状态估计的不确定性。协方差矩阵的大小反映了估计误差的大小。

卡尔曼滤波的数学表达式

卡尔曼滤波的数学表达式如下：

• 状态预测：( \hat{x}_k|k-1 = Fk \hat{x}{k-1|k-1} + B_k u_k )
• 协方差预测：( P_k|k-1 = Fk P{k-1|k-1} F_k^T + Q_k )
• 观测预测：( \hat{z}_k|k-1 = H_k \hat{x}_k|k-1 )
• 协方差预测：( R_k = H_k P_k|k-1 H_k^T + R_k )
• 卡尔曼增益：( K_k = P_k|k-1 H_k^T (H_k P_k|k-1 H_k^T + R_k)^{-1} )
• 状态更新：( \hat{x}_k|k = \hat{x}_k|k-1 + K_k (z_k - \hat{z}_k|k-1) )
• 协方差更新：( P_k|k = (I - K_k H_k) P_k|k-1 )

其中，( \hat{x}_k|k ) 表示在时间步 ( k ) 的状态估计，( z_k ) 表示在时间步 ( k ) 的观测值，( F_k ) 和 ( H_k ) 分别是状态转移矩阵和观测矩阵，( Q_k ) 和 ( R_k ) 分别是过程噪声和观测噪声协方差矩阵。

卡尔曼滤波的实时应用

卡尔曼滤波因其高效性和准确性，在实时应用中具有广泛的应用场景，以下是一些典型的应用实例：

• 导航系统：在GPS导航系统中，卡尔曼滤波器可以用于估计车辆的速度和位置，提高导航的精度和可靠性。
• 机器人导航：在机器人导航中，卡尔曼滤波器可以用于估计机器人的位置和姿态，帮助机器人避开障碍物并规划路径。
• 图像处理：在图像处理领域，卡尔曼滤波器可以用于去除图像噪声，提高图像质量。
• 生物医学信号处理：在生物医学信号处理中，卡尔曼滤波器可以用于分析生理信号，如心电图（ECG）和脑电图（EEG）。

结论

卡尔曼滤波器是一种强大的递归滤波器，其原理简单而有效。通过预测和更新步骤，卡尔曼滤波器可以减小估计误差，提高估计的准确性。随着技术的不断发展，卡尔曼滤波器在实时应用中的重要性将不断凸显，为各个领域带来更多的创新和进步。